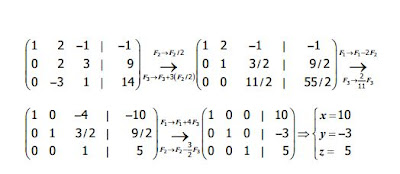BREVE INTRODUCCIÓN
El método de descomposición LU para la solución de sistemas de ecuaciones lineales debe su nombre a que se basa en la descomposición de la matriz original de coeficientes (A) en el producto de dos matrices (L y U).Esto es:

Donde:
L - Matriz triangular inferior
U - Matriz triangular superior con todos los elementos de la diagonal principal iguales a 1.
De lo anterior, para matrices de 3x3 se escribe:
Si efectuamos la multiplicación de L y U, igualando los elementos de ese producto con los de la matriz A correspondientes, se obtiene:

De aquí que los elementos de L y U son, en este caso:

Si el sistema de ecuaciones original se escribe como:
A x = b
lo cual resulta lo mismo escribir:
L U X = b
Definiendo a:
U X = Y
podemos escribir:
L Y = b
Resolviendo para Y, encontramos:

El algoritmo de solución, una vez conocidas L, U y b, consiste en encontrar primeramente los valores de "Y" por sustitución progresiva sobre "L Y = b". En segundo lugar se resuelve "U x = y " por sustitución regresiva para encontrar los valores de "x", obteniendo:

La determinación de los elementos de las matrices L y U se realizan eficientemente aplicando una forma modificada del método de eliminación de Gauss.
Se observa que el método de descomposición LU opera sólo sobre la matriz de coeficientes, sin modificar el vector de excitación (en este caso b), por lo que resulta superior al método de eliminación gausiana.
Ejemplo:
Resolver el siguiente sistema de ecuaciones, factorizando la matriz en LU:

 =
= 
Las matrices de factores L y U de A son:
L =  U =
U = 
El primer paso es resolver la ecuación L Y = b por sustitución progresiva para obtener los elementos del vector auxiliar Y:


 =
=
El segundo paso es resolver la ecuación U X = Y para encontrar los elementos de X, por sustitución regresiva:


 =
=
De donde se obtiene:











 =
= 






 U =
U =